Joyfrank
Lab Scientist : Am Still A Student
Wants to meet Laboratory Scientist : Just Want To Meet My Fellow Collegues
Articles
68
Followers
41
profile/92481597753291369.jpg
Joyfrank

PHILOSOPHY
~7.7 mins read
ToPhilosophy (from Greek: φιλοσοφία, philosophia, 'love of wisdom') is the study of general and fundamental questions about existence, knowledge, values, reason, mind, and language.Such questions are often posed as problemsto be studied or resolved. The term was probably coined by Pythagoras (c. 570 – 495 BCE). Philosophical methods include questioning, critical discussion, rational argument, and systematic presentation.

The School of Athens (1509–1511) by Raphael, depicting famous classical Greek philosophers in an idealized setting inspired by ancient Greek architecture
Classic philosophical questions include, "Is it possible to know anything?", and if so, "Can we prove it?"However, more practical and concrete questions may be posed, such as: "Is there a best way to live?", "Is it better to be just, even if one could get away with being unjust?",and "Do humans have free will?"
Historically, philosophy encompassed all bodies of knowledge and a practitioner was known as a philosopher.From the time of Ancient Greek philosopher Aristotle to the 19th century, "natural philosophy" encompassed astronomy, medicine, and physics.For example, Newton's 1687 Mathematical Principles of Natural Philosophy later became classified as a book of physics.
In the 19th century, the growth of modern research universities led academic philosophy and other disciplines to professionalize and specialize.In the modern era, some investigations that were traditionally part of philosophy became separate academic disciplines, including psychology, sociology, linguistics, and economics. Other investigations closely related to art, science, politics, or other pursuits remained part of philosophy. For example, is beauty objective or subjective?Does the scientific method reflect how science is actually practiced?What criteria separate science from pseudoscience? Is political utopia a hopeful dream or hopeless fantasy?
Major subfields of academic philosophy include metaphysics, which is concerned with the fundamental nature of existence and reality; epistemology, which studies the nature of knowledge and belief; ethics, which is concerned with moral value; and logic, which studies the rules of inference that allow one to deduce conclusions from true premises. Other notable subfields include philosophy of science, political philosophy, aesthetics, philosophy of language, and philosophy of mind.
The Main Branches of Philosophy are divided as to the nature of the questions asked in each area. The integrity of these divisions cannot be rigidly maintained, for one area overlaps into the others.
The Main Branches of Philosophy are divided as to the nature of the questions asked in each area. The integrity of these divisions cannot be rigidly maintained, for one area overlaps into the others.
Axiology: the study of value; the investigation of its nature, criteria, and metaphysical status. More often than not, the term "value theory" is used instead of "axiology" in contemporary discussions even though the term “theory of value” is used with respect to the value or price of goods and services in economics.
Some significant questions in axiology include the following:
Nature of value: is value a fulfillment of desire, a pleasure, a preference, a behavioral disposition, or simply a human interest of some kind?
Criteria of value: de gustibus non (est) disputandum (i.e., (“there's no accounting for tastes”) or do objective standards apply?
Status of value: how are values related to (scientific) facts? What ultimate worth, if any, do human values have?
Axiology is usually divided into two main parts.
Ethics: the study of values in human behavior or the study of moral problems: e.g., (1) the rightness and wrongness of actions, (2) the kinds of things which are good or desirable, and (3) whether actions are blameworthy or praiseworthy.
Consider this example analyzed by J. O. Urmson in his well-known essay, "Saints and Heroes":
"We may imagine a squad of soldiers to be practicing the throwing of live hand grenades; a grenade slips from the hand of one of them and rolls on the ground near the squad; one of them sacrifices his life by throwing himself on the grenade and protecting his comrades with his own body. It is quite unreasonable to suppose that such a man must be impelled by the sort of emotion that he might be impelled by if his best friend were in the squad."
Did the soldier who threw himself on the grenade do the right thing? If he did not cover the grenade, several soldiers might be injured or be killed. His action probably saved lives; certainly an action which saves lives is a morally correct action. One might even be inclined to conclude that saving lives is a duty. But if this were so, wouldn't each of the soldiers have the moral obligation or duty to save his comrades? Would we thereby expect each of the soldiers to vie for the opportunity to cover the grenade?
Æsthetics: the study of value in the arts or the inquiry into feelings, judgments, or standards of beauty and related concepts. Philosophy of art is concerned with judgments of sense, taste, and emotion.
E.g., Is art an intellectual or representational activity? What would the realistic representations in pop art represent? Does art represent sensible objects or ideal objects?
Is artistic value objective? Is it merely coincidental that many forms in architecture and painting seem to illustrate mathematical principles? Are there standards of taste?
Is there a clear distinction between art and reality?
Epistemology: the study of knowledge. In particular, epistemology is the study of the nature, scope, and limits of human knowledge.
Epistemology investigates the origin, structure, methods, and integrity of knowledge.
Consider the degree of truth of the statement, "The earth is round." Does its truth depend upon the context in which the statement is uttered? For example, this statement can be successively more accurately translated as …
"The earth is spherical"
"The earth is an oblate spheroid" (i.e., flattened at the poles).
But what about the Himalayas and the Marianas Trench? Even if we surveyed exactly the shape of the earth, our process of surveying would alter the surface by the footprints left and the impressions of the survey stakes and instruments. Hence, the exact shape of the earth cannot be known. Every rain shower changes the shape.
(Note here as well the implications for skepticism and relativism: simply because we cannot exactly describe the exact shape of the earth, the conclusion does not logically follow that the earth does not have a shape.)
profile/92481597753291369.jpg
Joyfrank
Update On Resumption Of School
~3.9 mins read
It's no longer news that there are some tertiary institutions or universities that have fixed a date for the reopening of schools and the resumption of academic activities within the university.


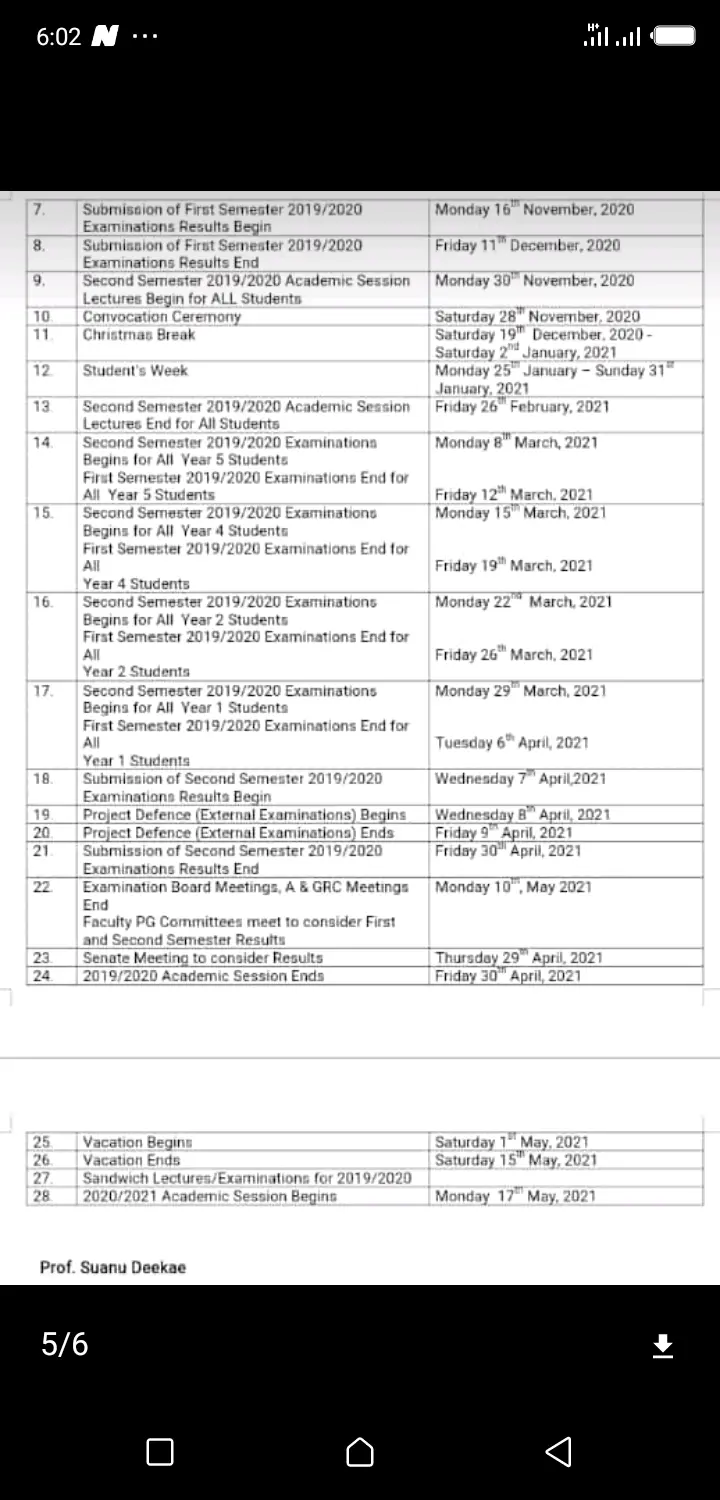

Despite the ASUU (Academic staff union of universities), these universities have passed memos across to their staffs and students telling them to come back to school on Monday (5/10/2020).
Nevertheless, in this article, I will show you the list of universities and states that will reopen school on Monday being 5th October 2020.
Here are the list of universities and states that will reopen on Monday.
1.Rivers State University.
One of the universities that have taken the bold step to reopen their school despite the ongoing ASUU strike is Rivers State University. Lately, Rivers state university passed or disseminated a memo through the registrar's (Dr Sydney C. Enyindah) office asking students to come back to school on Monday.
Here are evidence or proofs that shows the memo that was signed and stamped by the registrar of Rivers State University.
Also, some states in Nigeria have actually fixed a date for the resumption of academic activities in their tertiary institutions on Monday (5/10/2020).
Here are some of those states in Nigeria.
Note: The universities or tertiary institutions under ASUU might not commence their academic activities effectively due to the ongoing ASUU strike.
So, everyone should start getting ready to return back to school in case ASUU calls off the strike.
What is your take on University Resumption on Monday and what do you also think about this list of universities that will commence school activities on Monday?.
Leave your comments below and don't forget to share this post with your colleagues.
Also, follow my page for more meaningful updates.
Advertisement

Link socials
Matches
Loading...
